‘Numberless math’ gets kids thinking about and visualizing algebra

In elementary school, algebra involves using mathematical models to represent and analyze mathematical situations. (Shutterstock)
Today, elementary mathematics classrooms look and sound very different than what many parents may have experienced.
Many mathematics education researchers note that getting learners talking about mathematics and developing their own explanations is important.
To build students’ comfort and capabilities talking about math, sharing tasks that involve only pictures — what we call numberless or textless tasks — can elicit fascinating mathematical ideas. This puts learners in the driver’s seat,
noticing, wondering and actually doing mathematics for themselves.
Parents, caregivers and teachers can use these strategies to get learners
talking, explaining and visualizing important mathematical concepts while having quite a bit of fun!
Making kids notice and wonder
In our roles as mathematics education teachers at the university level (Marc and Evan) and in elementary school (Matthew), we all ask our students: “What do you notice?” and “What do you wonder?” to elicit mathematics conversations. This prompt is recommended by the National Council for Teachers of Mathematics.
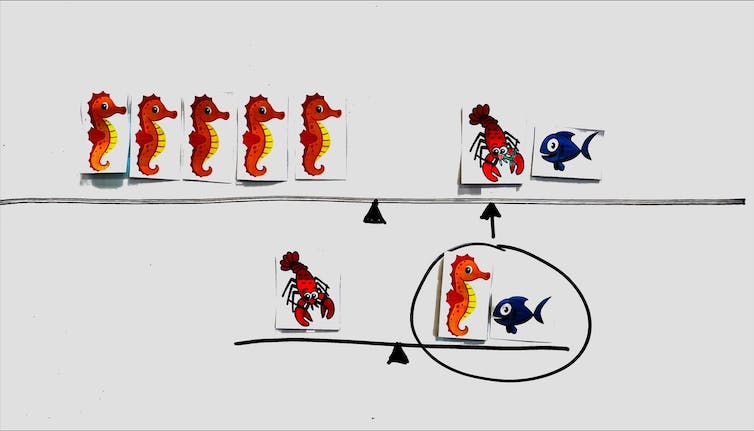
Suppose we were asking this question about the picture shown below that features two different lines of images with seahorses, lobster and fish (we’re Maritimers, after all).
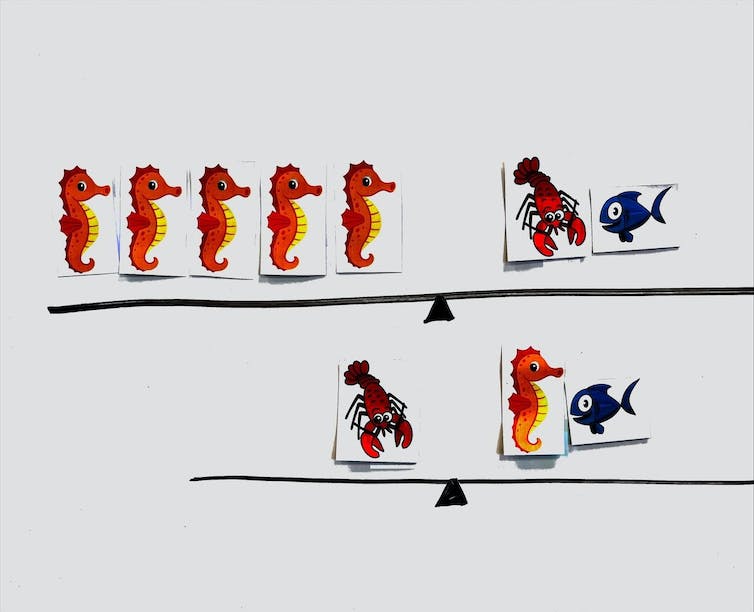
What do you notice?
(Marc Husband), Author provided
Almost immediately, we’d hear learners talk about mathematical ideas like these:
“It looks like a teeter-totter.”
“It’s a balance. The balance is even.”
“The right side of the scale weighs the same as the left side.”
“Five seahorses equals a lobster and a fish, and on the second balance, one lobster equals a seahorse and a fish.”
“These are two equations.”
These mathematical ideas provide the foundation for algebra. In elementary school, algebra involves using mathematical models: balances, in this case, to represent and analyze mathematical situations.
Invites kids to ask their own questions
Seeing the picture makes learners wonder and ask questions such as these: “What would happen to the balance if we removed a seahorse?” “How much does a seahorse weigh?” “How much does a fish weigh?”
We think this is significant because rather than the teacher or parent presenting questions for learners to solve, learners pose and investigate their own questions.
For example, we noticed students in our classrooms became super engaged in this task because the pictures prompted them to problem solve without us (their teachers) telling them the problem or how to solve it.
Now you try
Before reading further, try solving one of the above questions based on line one (with five seahorses), or line two (with one seahorse) with a friend or family member.
We recommend using paper cut-outs of the visual so you can move them around and record how you solved your problem.
Below are three different approaches for figuring out how much each item weighs.
Assigning different values
Learners assign values to the items and check whether their assigned guesses are true for each balance.
For example, if each seahorse is a one, a lobster might be two, and a fish might be three. We often hear, “Let’s check to see if this works on the second balance.”
When learners realize two does not equal three plus one, they reassign values to make the equation true. Interestingly, some learners guess by trying other numbers, such as one seahorse equals five or 10, and so on.
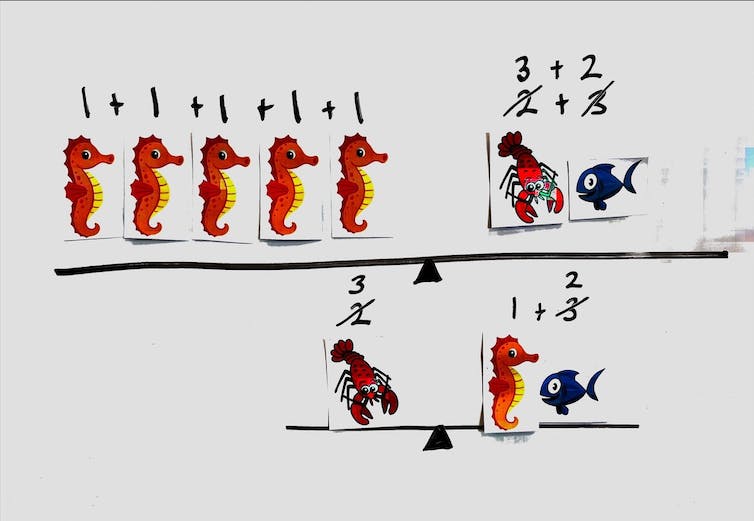
If five seahorses balance with one lobster and one fish, how might you start to think about their respective values?
(Marc Husband), Author provided
Combining balances
Learners combine balances by moving the items on the bottom to the top (or vice-versa) and then pulling items away to maintain the balance.
For example, the lobster in the second balance moves to the side of the five seahorses in the first balance, and the seahorse and fish move up to the fish and lobster side.
We hear learners say, “If we remove the lobsters on both sides and one seahorse from each side, it will stay in balance with four seahorses on one side and two fish on the other.”
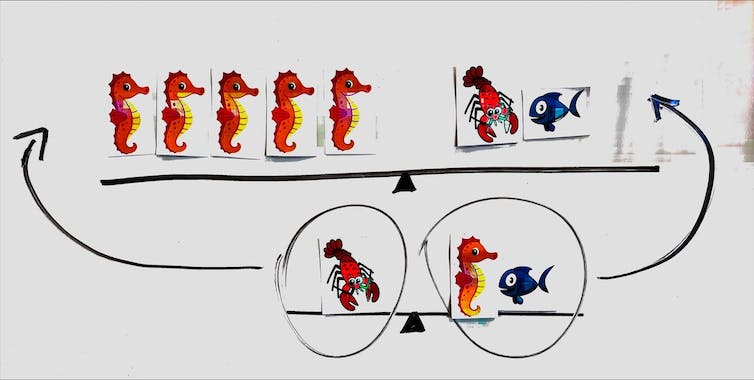
What about moving creatures on the bottom?
(Marc Husband), Author provided

The two balances combined.
(Marc Husband), Author provided
Could you remove items to maintain balance?
(Marc Husband), Author provided
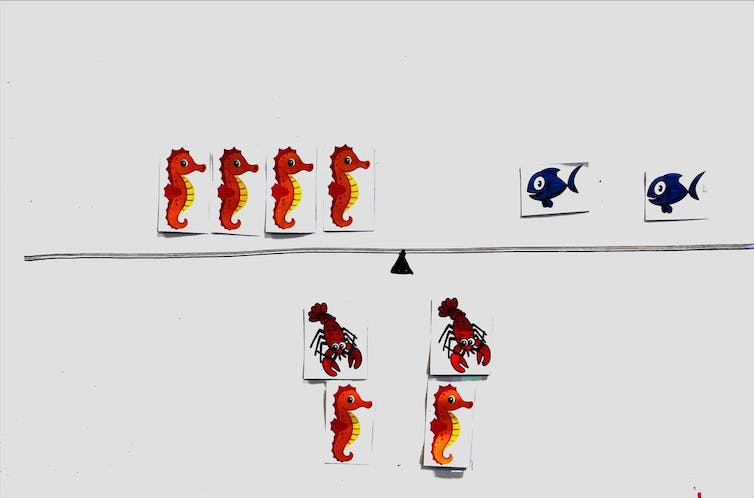
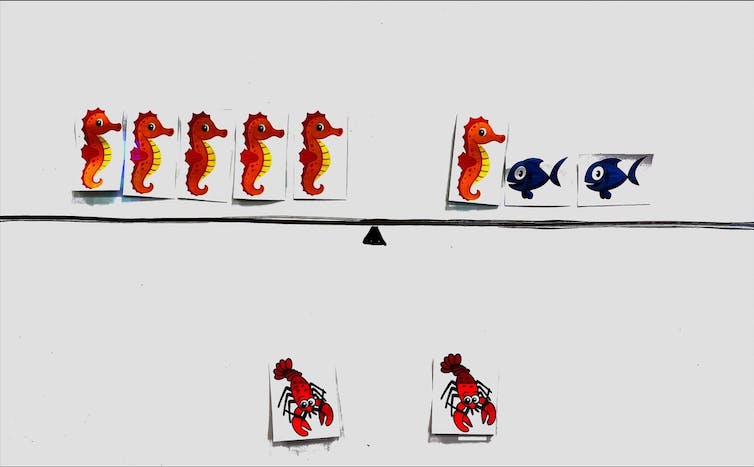
Based on this, learners often conclude that two seahorses equal one fish (or comparatively, for those who may be struggling still: a seahorse equals one, a fish equals two and a lobster equals five.
These approaches remind us that numberless/textless tasks get kids doing elimination in algebra without them knowing.
Exchanging pictures
Learners exchange the value of one picture with pictures of equal value. For example, seeing that a lobster is the same as a fish and a seahorse, learners replace the lobster in the first balance with a fish and an seahorse. This leads them to start pulling away, similar to the above strategy, taking one seahorse from each side and so on.
How about exchanging one lobster for one seahorse and one fish?
(Marc Husband), Author provided
Lobster and seahorse trade places.
(Marc Husband), Author provided

Now you could remove items to maintain balance.
(Marc Husband), Author provided
This approach reminds us that numberless/textless tasks get kids doing substitution in algebra without them knowing.
Learners in charge
We think selecting the right mathematics task for learners to work on with their peers is important because it engages them in fruitful conversations.
As the saying goes, “the person doing the talking is the person doing the learning”. Numberless/textless tasks get learners talking about mathematical ideas — in this case, with concepts like balance, same as and equal.
Learners actually see how to maintain balance by moving items on each side. This visual supports their understanding of an algebraic rule: “Whatever you do to one side of the equation, you need to do to the other side,” which parents might recall from memory.
This task sets the foundation for algebraic thinking without learners even knowing it. Algebra, often perceived as a scary word by many learners, becomes less scary through a numberless/textless task. This could be why many learners find themselves in the driver’s seat — talking, generating questions, visualizing and explaining mathematics!
![]()
The authors do not work for, consult, own shares in or receive funding from any company or organisation that would benefit from this article, and have disclosed no relevant affiliations beyond their academic appointment.






